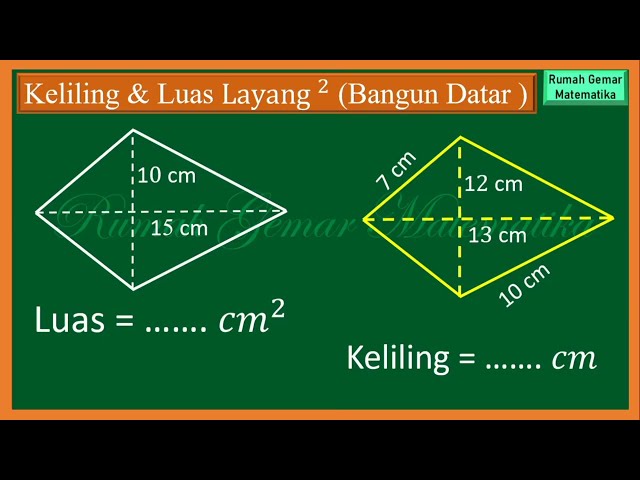
Rumus luas layang-layang adalah sebuah formula untuk menghitung luas layang-layang, sebuah bangun datar dua dimensi yang memiliki empat sisi sama panjang dan dua pasang sisi yang berlawanan sejajar. Misalnya, sebuah layang-layang dengan diagonal yang berukuran 10 cm dan 15 cm memiliki luas 75 cm persegi.
Rumus ini sangat penting dalam bidang matematika dan memiliki banyak manfaat. Rumus ini dapat digunakan untuk menghitung luas tanah, lapangan, dan bahkan sayap pesawat terbang. Selain itu, rumus ini juga memiliki sejarah yang menarik, pertama kali dikembangkan oleh matematikawan Yunani kuno Pythagoras.
Dalam artikel ini, kita akan membahas lebih dalam tentang rumus luas layang-layang, termasuk turunannya, aplikasi praktisnya, dan perkembangan historisnya.
Rumus Luas Layang-Layang
Rumus luas layang-layang merupakan aspek penting dalam matematika yang memiliki berbagai dimensi.
- Definisi
- Turunan
- Aplikasi
- Sejarah
- Sifat
- Kekurangan
- Kelebihan
- Contoh Soal
Aspek-aspek tersebut saling berkaitan dan membentuk pemahaman yang komprehensif tentang rumus luas layang-layang. Misalnya, mengetahui sejarahnya dapat memberikan konteks tentang bagaimana rumus tersebut dikembangkan dan pentingnya dalam perkembangan matematika.
Definisi
Definisi rumus luas layang-layang sangat penting untuk memahami konsep dan penggunaannya dalam matematika. Definisi ini memberikan dasar yang kuat untuk eksplorasi lebih lanjut tentang rumus ini.
-
Rumus Umum
Definisi rumus luas layang-layang secara umum dinyatakan sebagai L = (1/2) d1 d2, di mana L adalah luas layang-layang, d1 adalah panjang diagonal pertama, dan d2 adalah panjang diagonal kedua.
-
Sifat-Sifat Layang-Layang
Definisi rumus luas layang-layang terkait erat dengan sifat-sifat layang-layang itu sendiri, seperti memiliki empat sisi sama panjang dan dua pasang sisi yang berlawanan sejajar.
-
Aplikasi Praktis
Definisi rumus luas layang-layang juga mengarah pada berbagai aplikasi praktis, seperti menghitung luas tanah, lapangan, dan bahkan sayap pesawat terbang.
-
Sejarah dan Perkembangan
Definisi rumus luas layang-layang telah berkembang sepanjang sejarah, dengan kontribusi dari matematikawan seperti Pythagoras dan Euclid.
Dengan memahami definisi rumus luas layang-layang secara komprehensif, kita dapat membuka jalan untuk eksplorasi lebih mendalam tentang topik ini, termasuk turunan, aplikasi, dan implikasinya dalam berbagai bidang.
Turunan
Turunan merupakan salah satu aspek penting dalam memahami rumus luas layang-layang secara mendalam. Turunan memberikan pemahaman tentang bagaimana rumus tersebut diperoleh dan bagaimana rumus tersebut dapat diaplikasikan dalam berbagai situasi.
-
Dasar Geometris
Turunan rumus luas layang-layang didasarkan pada konsep geometri, yaitu sifat-sifat layang-layang dan hubungan antara diagonal-diagonalnya.
-
Proses Diferensiasi
Secara matematis, turunan rumus luas layang-layang melibatkan proses diferensiasi, yaitu mencari limit perubahan luas layang-layang terhadap perubahan panjang diagonal-diagonalnya.
-
Aplikasi Praktis
Turunan rumus luas layang-layang memiliki berbagai aplikasi praktis, seperti dalam arsitektur, teknik sipil, dan desain industri yang memerlukan perhitungan luas layang-layang yang akurat.
-
Generalisasi dan Perluasan
Turunan rumus luas layang-layang telah mengarah pada generalisasi dan perluasan konsep luas layang-layang, seperti rumus luas segitiga dan rumus luas trapesium.
Dengan memahami turunan rumus luas layang-layang, kita dapat memperoleh pemahaman yang lebih komprehensif tentang sifat-sifat layang-layang, proses diferensiasi, dan aplikasi praktisnya dalam berbagai bidang. Selain itu, turunan ini juga membuka jalan bagi pengembangan konsep luas bangun datar lainnya yang lebih kompleks.
Aplikasi
Aplikasi rumus luas layang-layang sangatlah luas dan mencakup berbagai bidang kehidupan. Rumus ini digunakan untuk menghitung luas bangun datar yang berbentuk layang-layang, yang memiliki empat sisi sama panjang dan dua pasang sisi yang berlawanan sejajar. Berikut adalah beberapa aspek penting terkait aplikasi rumus luas layang-layang:
-
Arsitektur
Rumus luas layang-layang digunakan untuk menghitung luas atap bangunan yang berbentuk layang-layang, sehingga dapat menentukan kebutuhan material dan biaya pembangunan.
-
Teknik Sipil
Dalam teknik sipil, rumus luas layang-layang digunakan untuk menghitung luas tanah atau lahan yang berbentuk layang-layang, sehingga dapat merencanakan tata ruang dan pembangunan infrastruktur secara efektif.
-
Desain Industri
Rumus luas layang-layang digunakan dalam desain industri untuk menghitung luas permukaan benda atau produk yang berbentuk layang-layang, seperti layang-layang itu sendiri, tenda, atau kanopi.
-
Matematika
Dalam matematika, rumus luas layang-layang menjadi dasar pengembangan rumus luas bangun datar lainnya, seperti segitiga dan trapesium, serta dalam menyelesaikan soal-soal geometri.
Aplikasi rumus luas layang-layang tidak terbatas pada bidang-bidang yang disebutkan di atas. Rumus ini juga dapat digunakan dalam bidang pertanian, geografi, seni, dan banyak lagi. Pemahaman yang baik tentang rumus luas layang-layang sangat bermanfaat dalam berbagai aspek kehidupan, baik secara praktis maupun teoritis.
Sejarah
Sejarah memiliki hubungan yang erat dengan perkembangan rumus luas layang-layang. Penemuan dan pengembangan rumus ini tidak terjadi dalam ruang hampa, melainkan dipengaruhi oleh peristiwa dan pemikiran historis yang signifikan.
Salah satu aspek penting dalam sejarah rumus luas layang-layang adalah kontribusi matematikawan Yunani kuno, Pythagoras. Pythagoras dikenal dengan teoremanya yang terkenal, yang juga berperan dalam pengembangan rumus luas layang-layang. Konsep perbandingan sisi-sisi dalam segitiga siku-siku yang dikemukakan Pythagoras memberikan dasar geometris untuk menghitung luas layang-layang.
Selain Pythagoras, matematikawan lain seperti Euclid dan Archimedes juga memberikan kontribusi pada perkembangan rumus luas layang-layang. Karya-karya mereka dalam bidang geometri dan pengukuran membantu menyempurnakan konsep luas layang-layang dan metodenya.
Memahami sejarah rumus luas layang-layang tidak hanya penting untuk mengapresiasi perkembangan matematika, tetapi juga memberikan konteks yang lebih kaya untuk memahami dan menerapkan rumus ini dalam kehidupan nyata. Dengan mengetahui asal-usul dan evolusi rumus ini, kita dapat lebih menghargai kegunaannya dan keterbatasannya.
Sifat
Dalam konteks rumus luas layang layang, sifat mengacu pada karakteristik dan kekhasan rumus tersebut yang membedakannya dari rumus luas bangun datar lainnya. Sifat-sifat ini memiliki implikasi penting dalam penerapan dan pemahaman rumus luas layang layang.
-
Generalisasi
Rumus luas layang layang merupakan generalisasi dari rumus luas segitiga. Dengan menggandakan luas segitiga dan membaginya dengan 2, kita memperoleh rumus luas layang layang. Sifat ini menunjukkan hubungan erat antara kedua bangun datar tersebut. -
Diagonal
Diagonal layang layang memiliki peran penting dalam menentukan luasnya. Panjang kedua diagonal harus diketahui untuk dapat menghitung luas layang layang. Sifat ini membedakan rumus luas layang layang dari rumus luas bangun datar lainnya yang tidak melibatkan diagonal. -
Kesamaan Sisi
Layang layang memiliki empat sisi yang sama panjang. Sifat ini memengaruhi cara menghitung luasnya, karena tidak diperlukan pengukuran panjang setiap sisi secara individual. Cukup mengetahui panjang salah satu sisi untuk menentukan keliling layang layang. -
Ketidakhadiran Sudut Siku-siku
Tidak seperti segitiga, layang layang tidak memiliki sudut siku-siku. Sifat ini menjadi pembeda utama dalam penerapan rumus luas, karena tidak dapat menggunakan konsep tinggi dan alas seperti pada segitiga.
Memahami sifat-sifat rumus luas layang layang sangat penting untuk menguasai penggunaan rumus tersebut secara efektif. Sifat-sifat ini memberikan landasan untuk pengembangan teorema dan aplikasi lebih lanjut dalam bidang matematika dan sains.
Kekurangan
Kekurangan rumus luas layang-layang perlu dipahami dengan baik untuk menghindari kesalahan dan keterbatasan dalam penggunaannya. Berikut beberapa kekurangan yang perlu diperhatikan:
-
Ketergantungan pada Diagonal
Rumus luas layang-layang membutuhkan panjang kedua diagonal untuk menghitung luas. Jika salah satu diagonal tidak diketahui atau sulit diukur, maka rumus ini tidak dapat diterapkan.
-
Ketidakmampuan Menghitung Luas Trapesium
Rumus luas layang-layang tidak dapat digunakan untuk menghitung luas trapesium, meskipun trapesium memiliki bentuk yang mirip. Hal ini karena rumus luas layang-layang hanya berlaku untuk bangun datar yang memiliki empat sisi sama panjang, sedangkan trapesium memiliki dua sisi sejajar yang panjangnya berbeda.
-
Keterbatasan pada Bangun Datar Kompleks
Rumus luas layang-layang hanya dapat digunakan untuk menghitung luas layang-layang sederhana. Untuk bangun datar yang lebih kompleks, seperti layang-layang dengan lengkungan atau potongan, rumus ini tidak dapat diterapkan.
-
Tidak Mempertimbangkan Sudut
Rumus luas layang-layang tidak mempertimbangkan sudut-sudut layang-layang. Akibatnya, rumus ini tidak dapat digunakan untuk menghitung luas layang-layang yang memiliki sudut tidak sama.
Memahami kekurangan rumus luas layang-layang sangat penting untuk memastikan penggunaannya secara tepat dan efektif. Dengan mengetahui keterbatasannya, kita dapat memilih metode alternatif yang lebih sesuai untuk menghitung luas bangun datar yang berbeda atau kompleks.
Kelebihan
Kelebihan rumus luas layang-layang terletak pada kesederhanaan dan kemudahan aplikasinya. Rumus ini hanya membutuhkan panjang kedua diagonal layang-layang, yang relatif mudah diukur atau diperoleh. Berbeda dengan rumus luas bangun datar lainnya, seperti segitiga atau trapesium, yang mungkin memerlukan pengukuran tambahan atau penggunaan rumus trigonometri yang lebih kompleks.
Kelebihan ini menjadikan rumus luas layang-layang sangat praktis dan efisien untuk digunakan dalam berbagai situasi. Misalnya, dalam arsitektur untuk menghitung luas atap bangunan yang berbentuk layang-layang, atau dalam teknik sipil untuk menentukan luas lahan yang akan dibangun. Kemudahan penggunaan rumus ini juga memungkinkan perhitungan cepat dan akurat, menghemat waktu dan meminimalkan kesalahan.
Selain itu, rumus luas layang-layang memiliki hubungan yang erat dengan konsep dasar geometri. Rumus ini diturunkan dari sifat-sifat layang-layang, seperti memiliki dua pasang sisi yang sama panjang dan dua diagonal yang saling tegak lurus. Pemahaman tentang hubungan ini tidak hanya membantu dalam menghafal rumus, tetapi juga memberikan dasar yang kuat untuk memahami konsep luas bangun datar secara keseluruhan.
Contoh Soal
Contoh soal merupakan komponen penting dalam materi rumus luas layang-layang karena memberikan kesempatan bagi siswa untuk mempraktikkan konsep dan prosedur yang telah dipelajari. Melalui contoh soal, siswa dapat menguji pemahaman mereka tentang rumus dan menerapkannya dalam situasi yang berbeda.
Contoh soal dalam rumus luas layang-layang biasanya melibatkan perhitungan luas layang-layang dengan panjang diagonal tertentu. Siswa harus menggunakan rumus L = (1/2) d1 d2, di mana L adalah luas layang-layang, d1 adalah panjang diagonal pertama, dan d2 adalah panjang diagonal kedua. Contoh soal dapat bervariasi dalam tingkat kesulitan, mulai dari soal dasar hingga soal yang lebih kompleks yang melibatkan penerapan konsep geometri lainnya.
Pemahaman tentang cara menyelesaikan contoh soal rumus luas layang-layang sangat penting dalam kehidupan nyata. Rumus ini memiliki banyak aplikasi praktis, seperti dalam arsitektur, teknik sipil, dan desain industri. Dengan menguasai contoh soal, siswa dapat mengembangkan keterampilan berpikir kritis, pemecahan masalah, dan akurasi dalam perhitungan yang dibutuhkan dalam berbagai profesi.
Pertanyaan yang Sering Diajukan tentang Rumus Luas Layang-Layang
Bagian ini menyajikan jawaban atas pertanyaan umum mengenai rumus luas layang-layang. Pertanyaan-pertanyaan ini mengantisipasi keraguan dan memberikan klarifikasi lebih lanjut tentang konsep dan aplikasi rumus.
Pertanyaan 1: Apa yang dimaksud dengan rumus luas layang-layang?
Rumus luas layang-layang adalah persamaan matematika yang digunakan untuk menghitung luas permukaan layang-layang, yaitu bangun datar dua dimensi dengan empat sisi sama panjang dan dua pasang sisi yang berlawanan sejajar.
Pertanyaan 2: Bagaimana cara menggunakan rumus luas layang-layang?
Untuk menggunakan rumus luas layang-layang, Anda perlu mengetahui panjang kedua diagonal layang-layang tersebut. Rumusnya adalah L = (1/2) d1 d2, di mana L adalah luas layang-layang, d1 adalah panjang diagonal pertama, dan d2 adalah panjang diagonal kedua.
Pertanyaan 3: Kapan rumus luas layang-layang digunakan?
Rumus luas layang-layang digunakan dalam berbagai aplikasi praktis, seperti menghitung luas atap bangunan, luas tanah, atau luas permukaan benda yang berbentuk layang-layang dalam desain industri.
Pertanyaan 4: Apakah rumus luas layang-layang hanya berlaku untuk layang-layang beraturan?
Tidak, rumus luas layang-layang berlaku untuk semua jenis layang-layang, baik layang-layang beraturan maupun tidak beraturan, selama memenuhi syarat memiliki empat sisi sama panjang dan dua pasang sisi yang berlawanan sejajar.
Pertanyaan 5: Bagaimana rumus luas layang-layang diturunkan?
Rumus luas layang-layang diturunkan dari konsep luas segitiga. Dengan membagi luas segitiga menjadi dua bagian yang sama, kita memperoleh rumus luas layang-layang.
Pertanyaan 6: Apa saja keterbatasan rumus luas layang-layang?
Keterbatasan rumus luas layang-layang adalah hanya dapat digunakan untuk menghitung luas layang-layang dan tidak dapat digunakan untuk menghitung luas bangun datar lainnya, seperti segitiga atau persegi panjang.
Kesimpulannya, memahami rumus luas layang-layang sangat penting untuk menerapkannya secara efektif dalam berbagai situasi. Pertanyaan yang dibahas dalam FAQ ini memberikan dasar yang komprehensif untuk menguasai rumus dan aplikasinya.
Selanjutnya, kita akan membahas topik terkait, yaitu sifat-sifat layang-layang yang memengaruhi penggunaan rumus luas layang-layang.
Tips Penting dalam Menguasai Rumus Luas Layang-Layang
Untuk menguasai rumus luas layang-layang dan menerapkannya secara efektif, berikut beberapa tips penting yang perlu diperhatikan:
Tip 1: Pahami Konsep Diagonal
Dalam rumus luas layang-layang, diagonal memiliki peran krusial. Pastikan Anda memahami konsep diagonal dan cara mengukurnya dengan benar.
Tip 2: Gunakan Rumus dengan Tepat
Rumus luas layang-layang adalah L = (1/2) d1 d2. Pastikan Anda menggunakan rumus ini dengan tepat dan memasukkan nilai diagonal yang benar.
Tip 3: Konversikan Satuan yang Sama
Satuan diagonal yang digunakan dalam rumus harus sama. Jika tidak, konversikan ke satuan yang sama (misalnya, cm atau m) sebelum menghitung luas.
Tip 4: Gambarkan Layang-Layang
Menggambar layang-layang dapat membantu Anda memvisualisasikan dan memahami konsep yang terkait dengan rumus luas layang-layang.
Tip 5: Berlatih dengan Contoh Soal
Memecahkan contoh soal secara teratur akan meningkatkan pemahaman Anda tentang rumus dan cara menggunakannya.
Tip 6: Identifikasi Sifat-Sifat Layang-Layang
Memahami sifat-sifat layang-layang, seperti sisi yang sama panjang dan diagonal yang tegak lurus, akan membantu Anda menyelesaikan soal yang lebih kompleks.
Menguasai tips ini akan memberikan Anda landasan yang kuat dalam menggunakan rumus luas layang-layang secara efektif dan akurat. Dengan memahami konsep dasar dan mempraktikkan tips ini, Anda akan dapat menerapkan rumus dengan percaya diri dalam berbagai situasi.
Pada bagian selanjutnya, kita akan mengeksplorasi aplikasi praktis rumus luas layang-layang dalam berbagai bidang, lebih lanjut memperkuat pentingnya menguasai rumus ini.
Kesimpulan
Rumus luas layang-layang merupakan formula penting dalam matematika dengan berbagai aplikasi praktis. Artikel ini telah mengeksplorasi rumus ini secara mendalam, mencakup turunan, sifat, kelebihan, dan contoh soal. Melalui pemahaman yang komprehensif tentang rumus ini, kita dapat menggunakannya secara efektif dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain industri.
Beberapa poin utama yang dibahas dalam artikel ini meliputi:
- Rumus luas layang-layang diturunkan dari sifat-sifat layang-layang, seperti sisi yang sama panjang dan diagonal yang saling tegak lurus.
- Rumus ini memiliki kelebihan dalam kesederhanaan dan kemudahan aplikasinya, hanya membutuhkan panjang kedua diagonal layang-layang.
- Pemahaman tentang rumus luas layang-layang sangat penting untuk menyelesaikan soal-soal matematika dan untuk aplikasi praktis dalam berbagai bidang.
Menguasai rumus luas layang-layang tidak hanya meningkatkan kemampuan matematika kita, tetapi juga membekali kita dengan alat yang berharga untuk memecahkan masalah di dunia nyata. Mari kita manfaatkan rumus ini untuk eksplorasi lebih lanjut, inovasi, dan kemajuan dalam berbagai bidang.